Answer:
(1) -
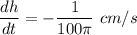
(2) -

Explanation:
To solve this problem, we can use the concept of related rates and the formulas for the volume and surface area of a sphere. Let's denote the radius of the ice layer as "r" and the thickness of the ice layer as "h."

Given:
Radius of the copper ball, r = 20 cm
Rate of ice melting, dV/dt = -25 cm^3/min
Find:
(1) - The rate at which the thickness of the ice layer is decreasing, dh/dt when it is 5 cm thick.
(2) - The rate at which the outer surface area of the ice layer is decreasing (dA/dt).

The volume of the ice layer can be expressed as the difference between the volume of the outer sphere (with the ice layer) and the volume of the inner sphere (without the ice layer):
![V = \frac4\pi \Big[(r + h)^3 - r^3\Big]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y9dqoh8qipxrm7k19zjrgvfy5aayos1iwe.png)
Differentiate this with respect to time, t.
![V = \frac43\pi\Big[(r + h)^3 - r^3\Big]\\\\\\\Longrightarrow (dV)/(dt) =(d)/(dt) \Big[ \frac43\pi\Big[(r + h)^3 - r^3\Big]\Big]\\\\\\\Longrightarrow (dV)/(dt) =\frac43\pi \Big[(3(r + h)^2)((dh)/(dt) ) - 0\Big]\\\\\\\Longrightarrow \boxed{(dV)/(dt) =4\pi(r + h)^2(dh)/(dt)}](https://img.qammunity.org/2024/formulas/mathematics/high-school/nqh9oalhhlkkq7z00vixodv4tie8swy77z.png)
Plug in dV/dt, r, and h and solve for dh/dt
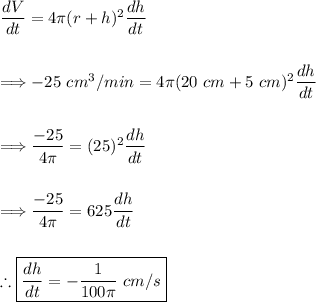
Thus, the first part is solved. The negative shows that the thickness is decreasing with time. The question may ignore that negative.
The outer surface of the ball is given as:
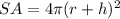
Differentiate the function with respect to time, t.
![SA = 4\pi(r + h)^2\\\\\\\Longrightarrow (dA)/(dt)=(d)/(dt)\Big[4\pi(r + h)^2\Big] \\\\\\\Longrightarrow \boxed{(dA)/(dt)=8\pi(r + h)(dh)/(dt) }](https://img.qammunity.org/2024/formulas/mathematics/high-school/xqd7tduetiw5ffqjd61txjqw42f3muy9tg.png)
Substitute in our known values.
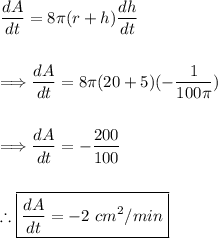
Thus, the second part is solved. Once again, the question may want you to disregard the negative.