Question

NO LINKS!!! URGENT HELP PLEASE!!

You roll a 6-sided die 30 times. The table shows the results.

a. What is the theoretical probability of 5?

b. What is the experimental probability of rolling a 5?

c. Why are the probabilities found in parts (a) and (b) different?​

Answer 1

a. The theoretical probability of rolling a 5 on a fair 6-sided die is 1/6. This is because there are six equally likely outcomes (numbers 1 through 6), and only one of them is a 5.

b. To find the experimental probability of rolling a 5, we need to count the actual occurrences of 5 in the 30 rolls and divide it by the total number of rolls. Let's say the number of times a 5 was rolled was 6. Then the experimental probability would be 6/30, which simplifies to 1/5.

c. The probabilities found in parts (a) and (b) are different because theoretical probability is based on the assumption of an idealized, fair die where all outcomes have equal likelihood. On the other hand, experimental probability is based on the actual outcomes observed in a specific set of trials. In real-world situations, the experimental probability may differ from the theoretical probability due to factors like chance, sampling error, or variations in the way the die is rolled.

Note: It would really mean the world to me if I received a special thanks from anyone viewing!!!

Answer 2

`\textsf{a)} \quad (1)/(6)`

`\textsf{b)} \quad (1)/(5)`

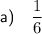
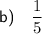
c) See below.

Explanation:

Part a

Theoretical probability refers to the likelihood of an event occurring based on assumptions, rather than observed data. It is calculated by dividing the number of favourable outcomes by the total number of possible outcomes.

For a fair 6-sided die, the theoretical probability of rolling a 5 can be calculated by dividing the number of favorable outcomes (rolling a 5) by the total number of possible outcomes (the numbers 1 to 6):

`\sf P(X=5)=(1)/(6)`

`\hrulefill`

Part b

Experimental probability is based on the actual results of an experiment (gathered by experimenting repeatedly). It is calculated by dividing the recorded number of times an event happens by the total number of trials in the actual experiment.

From the given table, we can see that a 5 was rolled 6 times in a trial of 30 rolls. Therefore, the experimental probability of rolling a 5 can be calculated by dividing the recorded number of times a 5 was rolled (6 times) by the total number of trials (30):

`\sf P(X=5)=(6)/(30)=(1)/(5)`

`\hrulefill`

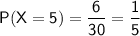
Part c

The probabilities found in parts (a) and (b) are different because the theoretical probability is based on mathematical calculations and assumes that the die is fair, with all outcomes equally likely. On the other hand, the experimental probability is obtained through actual observations and can be influenced by various factors such as chance variations, sample size, or possible biases. In this case, the experimental probability is slightly higher than the theoretical probability due to chance fluctuations in the small sample size of 30 rolls. With more rolls, the experimental probability would tend to converge towards the theoretical probability.