Question

Find the angle between vector bold lower u equals 3 bold lower I plus start root 3 end root bold lower j and vector bold lower v equals negative 2 bold lower I minus 5 bold lower j to the nearest degree. A. 82° B. 38° C. 142° D. 98°

Answer 1

C. 142°

Explanation:

You want the angle between vectors u=3i+√3j and v=-2i-5j.

Angle

There are a number of ways the angle between the vectors can be found. For example, the dot-product relation can give you the cosine of the angle:

u•v = |u|·|v|·cos(θ) . . . . . . where θ is the angle of interest

You can find the angles of the vectors individually, and subtract those:

u = |u|∠α

v = |v|∠β

θ = α - β

When the vectors are expressed as complex numbers, the angle between them is the angle of their quotient:

`\frac{\vec{u}}{\vec{v}}=\frac{|\vec{u}|\angle\alpha}{|\vec{v}|\angle\beta}=\frac{|\vec{u}|}{|\vec{v}|}\angle(\alpha-\beta)=\frac{|\vec{u}|}{|\vec{v}|}\angle\theta`

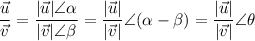
This method is used in the calculation shown in the first attachment. The angle between u and v is about 142°.

A graphing program can draw the vectors and measure the angle between them. This is shown in the second attachment.

__

Additional comment

The approach using the quotient of the vectors written as complex numbers is simply computed using a calculator with appropriate complex number functions. There doesn't seem to be any 3D equivalent.

The dot-product relation will work with 3D vectors as well as 2D vectors.

<95141404393>