Question

What is the present value of a cash flow stream of $1,000 per year annually for 12 years that then grows at 4.6 percent per year forever when the discount rate is 13 percent? Note: Round intermediate calculations and final answer to 2 decimal places.

Answer 1

The present value of a cash flow stream of $1,000 per year for 12 years that then grows at 4.6% annually forever, with a discount rate of 13%, is calculated by summing the present value of the 12-year annuity and the present value of the growing perpetuity that starts after the 12th year.

Step-by-step explanation:

Calculating the Present Value of a Cash Flow Stream

To calculate the present value of a cash flow stream of $1,000 per year for 12 years with growth at a rate of 4.6 percent thereafter, and using a discount rate of 13 percent, we first find the present value of the initial 12-year annuity and then calculate the perpetual value that starts after the 12th year and grows at 4.6 percent. The present value of an annuity can be calculated using the present value of an annuity formula while the perpetual value is calculated as a perpetuity with growth using the formula PV = C / (r - g), where C represents the yearly payment, r the discount rate, and g the growth rate.

For the initial 12-year period, the present value formula for an annuity is used. For the growth perpetuity that follows, the first payment will be $1,000 (the amount in the 12th year) multiplied by 1.046 (to account for the 4.6 percent growth), and this value is then divided by the excess of the discount rate over the growth rate (13% - 4.6% = 8.4%). Summing the values from both parts gives us the overall present value of the cash flow stream.

Going back to the example provided, if a simple two-year bond was issued for $3,000 at an 8% interest rate and pays $240 in interest each year, its present value can be calculated using the discount rate. The calculations are as shown in Table C2, taking the future cash payments back to their present discounted value using the formula. If interest rates rise, changing the discount rate to 11%, this will decrease the present value of those future cash payments.

Answer 2

The present value of the cash flow stream, rounded to 2 decimal places, is approximately $18,051.71.

How to calculate present value of a cash flow

Present Value of the Annuity for 12 Years:

Given:

Cash flow per year: $1,000

Discount rate: 13%

Number of years: 12

Using the annuity formula:

$1,000 × [(1 -
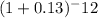`(1 + 0.13)^-12`) / 0.13]

≈ $5,856.59

Present Value of the Perpetuity Beyond 12 Years:

Cash flow in perpetuity (at the end of the 12th year): $1,000

Discount rate: 13%

Growth rate of perpetuity: 4.6%

Perpetuity formula: $1,000 / (0.13 - 0.046)

≈ $12,195.12

Total Present Value:

The total present value is the sum of the present value of the annuity and the perpetuity:

$5,856.59 + $12,195.12 ≈ $18,051.71

Therefore, the present value of the cash flow stream, rounded to 2 decimal places, is approximately $18,051.71.