Question

You are given a triangle with side lengths of 6, 9, and 12. Is the triangle a right triangle? How do you know?

Answer 1

I’m happy to help!
Right triangle lengths can be checked by the Pythagorean theorem.
This states that a^2+b^2=c^2
a and b are the shorter side lengths, and they form the right angle. c is the hypotenuse, and is the longest length.
Input the values to check if the equation checks out:
6^2+9^2=12^2
36+81=144
117≠144
No, it is not a right triangle. Hope this helps!

Answer 2

No, it's not

Explanation:

You choose the longest side which is 12 and apply the theory of phitagors

The longest side which is the hypotenuse in a right triangle = square root the square sum for each side

So to be a right triangle it should be

`\sqrt{ {9}^(2) + {6}^(2) } = 10.8 \: \: that \: doesnt \: equal \: 12`

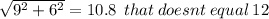
So it's not a right triangle.

Look at the famous right triangle whose side are 5(hypotenuse), 4, 3

`\sqrt{ {4}^(2) + {3}^(2) } = 5`

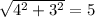
So it's a right triangle