Hello !
Answer:
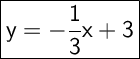
Explanation:
The slope-intercept form of a line equation is
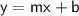 where m is the slope and b is the y-intercept.
where m is the slope and b is the y-intercept.
The slope of the line ( with
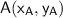 and
and
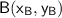 ) is given by
) is given by
 .
.
Given :
Let's calculate the slope :
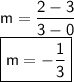
The y-intercept is the value of y when x = 0.
According to the graph,
 .
.
Let's replace m and b with their values in the formula :
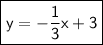
Have a nice day ;)