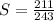Question

Which equation could be used to calculate the sum of geometric series?

1/3+2/9+4/27+8/81+16/243

Answer 1

The sum of a geometric series can be calculated using the following equation:

`S= (a(1-r^(n) ))/(1-r)`

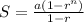
Where:

S is the sum of the series,

a is the first term of the series,

r is the common ratio, and

n is the number of terms in the series.

In the given geometric series,
`(1)/(3) + (2)/(9) + (4)/(27) +(8)/(81) +(16)/(243)`,

the first term, a =
`(1)/(3)`,

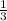the common ratio, r =
`(2)/(3)`,

and the no. of terms,
`n=5`

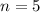
Therefore using the equation, we can calculate the sum, S:

`S= (1)/(3) ((1-((2)/(3))^(5) ))/(1-(2)/(3) )`

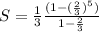
Simplifying the equation gives:

or,
`S= (1)/(3) ((1-(32)/(243)))/((1)/(3) )`

or,
`S= (1)/(3) (((211)/(243)))/((1)/(3) )`

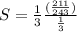
Therefore,
`S= {(211)/(243)`
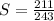
Hence the sum of the given geometric series is
`S= (211)/(243)}`

Answer 2

Answer:0.868312752

rounded to 0.87

Explanation: