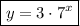Question

NO LINKS!! URGENT HELP PLEASE!!

Please help me with #25 and 26​

Answer 1

`\textsf{25)} \quad y=6\cdot 2^x`

`\textsf{26)}\quad y=3\cdot 7^x`

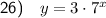
Explanation:

The general form of an exponential function is:

`\boxed{y=ab^x+c}`

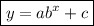
where:

• a is the initial value (y-intercept).
• b is the base (growth/decay factor) in decimal form.
• y=c is the horizontal asymptote.
• x is the independent variable.
• y is the dependent variable.

As the asymptote is y = 0 for both equations, the general function to use is:

`\boxed{y=ab^x}`

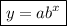
To write the equation of an exponential function that passes through the given pairs of points, substitute both points into the exponential function and solve to find the values of a and b.

`\hrulefill`

Question 25

Given points:

• (0, 6)
• (3, 48)

Substitute point (0, 6) into the formula and solve for a:

`\begin{aligned}y&=ab^x\\\implies 6&=ab^0\\6&=a(1)\\a&=6\end{aligned}`

Substitute the found value of a and the point (3, 48) into the formula and solve for b:

`\begin{aligned}y&=ab^x\\\implies48&=6b^3\\8&=b^3\\b&=\sqrt[3]{8}\\b&=2\end{aligned}`

Therefore, the exponential equation with asymptote y = 0 that passes through points (0, 6) and (3, 48) is:

`\boxed{y=6\cdot 2^x}`

`\hrulefill`

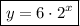
Question 26

Given points:

• (1, 21)
• (2, 147)

Substitute point (1, 21) into the formula, and point (2, 147) into the formula, to create two equations:

`21=ab^1 \implies ab=21`

`147=ab^2 \implies ab^2=147`

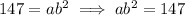
Divide the second equation by the first equation to eliminate a and solve for b:

`(ab^2)/(ab)=(147)/(21)`

`(b^2)/(b)=7`

`b=7`

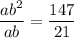
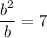
Substitute the found value of b into the first equation and solve for a:

`\begin{aligned}ab&=21\\7a&=21\\a&=3\end{aligned}`

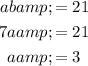
Substitute the found values of a and b into the formula to write an exponential equation with asymptote y = 0 that passes through points (1, 21) and (2, 147):

`\boxed{y=3\cdot 7^x}`