Question

Are the following statements true or false? ? 1. The line parametrized by x = 7, y = 5t, z=6+t is parallel to the x-axis. ? 2. The parametric curve x = (3t+4)2, y = 5(3t+4)2-9, for 0 ≤t≤ 3 is a line segment. ? 3. A parametrization of the graph of y = ln(x) for a > 0 is given by a = e', y = t for -[infinity]

Answer 1

Regarding the given statements:

Statement 1 is false.

Statement 2 is true.

Statement 3 is false.

How to determine the validity of the statements

Analyze each statement:

The line parametrized by x = 7, y = 5t, z = 6 + t has a constant x-value of 7.

Since the x-axis only includes points where x = 0, the line cannot be parallel to the x-axis. Therefore, the statement is false.

The parametric curve
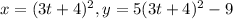`x = (3t + 4)^2, y = 5(3t + 4)^2 - 9`, for 0 ≤ t ≤ 3, represents a line segment. T

he parameter t ranges from 0 to 3, which means it covers a specific interval. Therefore, the curve represents a line segment within that interval. Thus, it is true

The given parametrization,
`x = e^t`, y = t, defines a curve where x grows exponentially while y increases linearly.

This doesn't match the graph of y = ln(x), where y grows logarithmically with x. Hence the statement is false.