Answer:
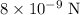 .
.
Step-by-step explanation:
By Coulomb's Law, the magnitude of electrostatic force between two point charges is:
 ,
,
Where:
 is Coulomb's Constant,
is Coulomb's Constant,
 and
and
 are the magnitudes of the two charges, and
are the magnitudes of the two charges, and
 is the distance between the two charges.
is the distance between the two charges.
In this question, assume that the magnitude of the two point charges were originally
 and
and
 with a distance of
with a distance of
 in between.
in between.
Assume that
 becomes
becomes
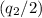 and
and
 becomes
becomes
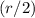 . By Coulomb's Law, the magnitude of the electrostatic force between the two new charges would become:
. By Coulomb's Law, the magnitude of the electrostatic force between the two new charges would become:
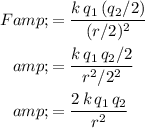 .
.
In other words, magnitude of the force between the two new charges would be twice that of the original value. The magnitude of the new force would be
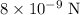 .
.