Question

How do I do the second part​

Answer 1

a) See below for proof.

b) Area of the original playground = 1200 m²

Explanation:

Part (a)

From observation of the given diagram, the width of the original rectangular playground is x metres, and the length is 3x metres.

As the area of a rectangle is the product of its width and length, then the expression for the area of the original playground is:

`\begin{aligned}\textsf{Area}_(\sf original)&=\sf width \cdot length\\&=x \cdot 3x \\&= 3x^2\end{aligned}`

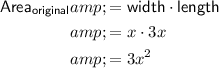
Given the width of the extended playground is 10 metres more than the width of the original playground, and the length is 20 metres more than the original playground, then the width is (x + 10) metres and the length is (3x + 20) metres. Therefore, the expression for the area of the extended playground is:

`\begin{aligned}\textsf{Area}_(\sf extended)&=\sf width \cdot length\\&=(x+10)(3x+20)\\&=3x^2+20x+30x+200\\&=3x^2+50x+200\end{aligned}`

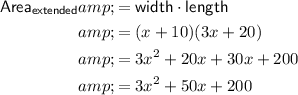
If the area of the larger extended playground is double the area of the original playground then:

`\begin{aligned}2 \cdot \textsf{Area}_(\sf original)&=\textsf{Area}_(\sf extended)\\2 \cdot 3x^2&=3x^2+50x+200\\6x^2&=3x^2+50x+200\\6x^2-3x^2-50x-200&=3x^2+50x+200-3x^2-50x-200\\3x^2-50x-200&=0\end{aligned}`

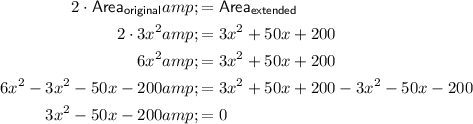
Hence showing that 3x² - 50x - 200 = 0.

`\hrulefill`

Part (b)

To calculate the area of the original playground, we first need to solve the quadratic equation from part (a) to find the value of x.

We can use the quadratic formula to do this.

`\boxed{\begin{minipage}{5 cm}\underline{Quadratic Formula}\\\\$x=(-b \pm √(b^2-4ac))/(2a)$\\\\when $ax^2+bx+c=0$ \\\end{minipage}}`

When 3x² - 50x - 200 = 0, then:

• a = 3
• b = -50
• c = -200

Substitute the values of a, b and c into the quadratic formula:

`x=(-(-50)\pm√((-50)^2-4(3)(-200)))/(2(3))`

`x=(50\pm√(2500+2400))/(6)`

`x=(50\pm√(4900))/(6)`

`x=(50\pm70)/(6)`

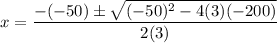
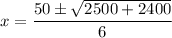
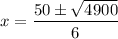
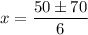
So the two solutions for x are:

`x=(50+70)/(6)=(120)/(6)=20`

`x=(50-70)/(6)=-(20)/(6)=-3.333...`

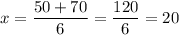
The width of the original playground is x metres. As length cannot be negative, this means that the only valid solution to the quadratic equation is x = 20.

To find the area of the original playground, substitute the found value of x into the equation for the area:

`\begin{aligned}\textsf{Area}_(\sf original)&=3x^2\\&=3(20^2)\\&=3(400)\\&=1200\; \sf m^2\end{aligned}`

Therefore, the area of the original playground is 1200 m².