Question

1.) The angle of depression from the top of the flag pole on top of a light house to a boat ion the ocean is 3.3 degrees. The angle of depression from the bottom of the flagpole to the boat is 2.6 degrees. If the boat is 400ft away from the shore and the lighthouse is right on the edge of the shore, how tall is the flag pole? Round answer to the nearest 10th.

Answer 1

To find the height of the flagpole, we can use the trigonometric concept of the angle of depression.

Let's denote the height of the flagpole as
`\sf h \\`.

From the top of the lighthouse, the angle of depression to the boat is 3.3 degrees, and the distance from the boat to the shore is 400 ft. This forms a right triangle with the height of the flagpole as the opposite side and the distance from the boat to the shore as the adjacent side.

Using the tangent function:

`\sf \tan(3.3^\circ) = (h)/(400) \\`

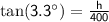
Solving for
`\sf h \\`:

`\sf h = 400 \cdot \tan(3.3^\circ) \\`

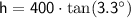
Similarly, from the bottom of the flagpole, the angle of depression to the boat is 2.6 degrees. This forms another right triangle, but this time the height of the flagpole is the adjacent side and the distance from the boat to the shore is the opposite side.

Using the tangent function:

`\sf \tan(2.6^\circ) = (h)/(400) \\`

Solving for
`\sf h \\`:

`\sf h = 400 \cdot \tan(2.6^\circ) \\`

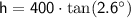
To find the total height of the flagpole, we can sum up the two heights:

`\sf \text{Total height} = h_{\text{top}} + h_{\text{bottom}} \\`

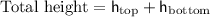
Substituting the respective values:

`\sf \text{Total height} = 400 \cdot \tan(3.3^\circ) + 400 \cdot \tan(2.6^\circ) \\`

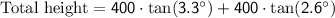
Using a calculator, we find:

`\sf \text{Total height} \approx 38.4 + 31.5 \approx 69.9 \\`

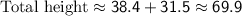
Rounding to the nearest tenth:

`\sf \text{Total height} \approx 69.9 \, \text{ft} \\`

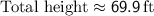
Therefore, the height of the flagpole is approximately 69.9 ft.