Question

The angle of elevation from a point 200 feet away on the street to the top of a building is 29 degrees. To the nearest foot, how tall is the building?

Answer 1

To find the height of the building, we can use the trigonometric concept of the angle of elevation.

Let's denote the height of the building as
`\sf h \\`.

From a point 200 feet away on the street, the angle of elevation to the top of the building is 29 degrees. This forms a right triangle with the height of the building as the opposite side and the distance from the point on the street to the building as the adjacent side.

Using the tangent function:

`\sf \tan(29^\circ) = (h)/(200) \\`

Solving for
`\sf h \\`:

`\sf h = 200 \cdot \tan(29^\circ) \\`

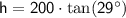
Using a calculator, we find:

`\sf h \approx 200 \cdot 0.5543 \approx 110.86 \\`

Rounding to the nearest foot:

`\sf h \approx 111 \, \text{ft} \\`

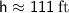
Therefore, the height of the building is approximately 111 feet.