Question

NO LINKS!! URGENT HELP PLEASE!!

Find the value of x of both circles, please!!

Answer 1

1) x = 39

2) x = 62

Explanation:

Question 1

The sum of all arc measures of a circle is 360°.

Therefore, to find the measure of the unlabelled intercepted arc, subtract the measures of the other two arcs from 360°:

`360^(\circ)-160^(\circ)-122^(\circ)=78^(\circ)`

Therefore, the measure of the unlabelled intercepted arc is 78°.

To find the measure of the inscribed angle, x, we can use the Inscribed Angle Theorem. This theorem states that the measure of an inscribed angle is half the measure of the intercepted arc. Therefore, the inscribed angle x is half of 78°:

`x^(\circ)=(78^(\circ))/(2)=39^(\circ)`

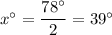
Therefore, the value of x is 39.

`\hrulefill`

Question 2

To find the value of x, we can use the Intersecting Secants Theorem.

Intersecting Secants Theorem

If two secant segments are drawn to the circle from one exterior point, the measure of the angle formed by the two lines is half of the (positive) difference of the measures of the intercepted arcs.

From inspection of the given diagram:

• The angle formed by the two secants is 42.5°.
• The two intercepted arcs are 147° and x°.

Therefore, according to the Intersecting Secants Theorem:

`42.5^(\circ)=(1)/(2)(147^(\circ)-x^(\circ))`

`2 \cdot 42.5^(\circ)=2 \cdot (1)/(2)(147^(\circ)-x^(\circ))`

`85^(\circ)=147^(\circ)-x^(\circ)`

`x^(\circ)=147^(\circ)-85^(\circ)`

`x^(\circ)=62^(\circ)`

`x=62`

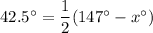
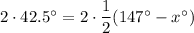
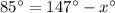
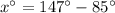
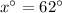
Therefore, the value of x is 62.