Question

For an enclosed gas with a constant temperature, the pressure of the gas changes from 15 atm to 30 atm. What happens to the volume of the gas?

Answer 1

Answer: The volume of an ideal gas will decrease if the pressure increases.

Step-by-step explanation:

To answer this question, we need to use the Ideal Gas Law:

`PV = nRT`

The "mathematical" way of solving this is to solve the equation for the variable we are interested in. In this case, we want to know about the volume, so get V by itself:

`V = (nRT)/(P)`

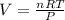
By inspecting the formula, we can see that n, R, and T are in the numerator, while P is in the denominator. Mathematically speaking, if the numerator changes the SAME change will happen to V; if the denominator changes the OPPOSITE change will happen to V.

For example,

• If n increases, the same thing happens to V. V increases.
• If T increases, the same thing happens to V. V increases.
• If n decreases, the same thing happens to V. V decreases.
• If T decreases, the same thing happens to V. V decreases.

But, for the denominator,

• If P increases, the OPPOSITE thing happens to V. V decreases.
• If P decreases, the OPPOSITE thing happens to V. V increases.

So, since the questions says that the pressure changes from 15 atm to 30 atm (an INCREASE), the volume will do the OPPOSITE thing and decrease.

General Patterns:

The following are general patterns for the Ideal Gas Law:

• P does the SAME thing as n and T.
• P does the OPPOSITE thing as V.
  
• V does the SAME thing as n and T.
• V does the OPPOSITE thing as P.
  
• n does the SAME thing as P and V.
• n does the OPPOSITE thing as T.
  
• T does the SAME thing as P and V.
• T does the OPPOSITE thing as n
  
• R is a constant so it never changes.