Question

If the equilibrium

constant of a given reaction is 4.85, what is the equilibrium constant of its reverse reaction?

Answer 1

Answer: The equilibrium constant of its reverse reaction is 0.206.

Step-by-step explanation:

For a given reaction if, the forward reaction has an equilibrium constant of
`K_c`, then the reverse reaction has an equilibrium constant of
`1/K_c`.

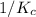In the question,
`K_c=4.85`. Therefore, the reverse reaction has an equilibrium constant of
`1/4.85 = 0.206`.

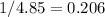More Details:

You can show yourself that this rule works, by the following process.

Suppose you have a chemical reaction given by:

`a \ A + b \ B \rightarrow c \ C + d \ D`

Then, the equilibrium constant for this reaction is given by the formula:

`K_c=([C]^c[D]^d)/([A]^a[B]^b)`

On the other hand, the reverse reaction is given by:

`c \ C + d \ D \rightarrow a \ A + b \ B`

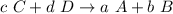
Then, the reverse reaction's equilibrium constant is:

`K_r=([A]^a[B]^b)/([C]^c[D]^d)`

But this is the same as the original constant, except it's flipped over! Mathematically, speaking:

`K_r = ([A]^a[B]^b)/([C]^c[D]^d) = 1 / ([C]^c[D]^d)/([A]^a[B]^b) = 1 / K_c = 1 / K_c`