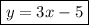Question

CAN SOMEONE PLLSSS HELP ME WITH THIS PROBLEM

Answer 1

`y = 3x - 5`

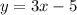
Explanation:

We can write the equation of the line we are trying to solve for in point-slope form, then convert it to slope-intercept form.

Point-slope form is:

`y - b = m(x - a)`

where
`m` is the line's slope and
`(a, b)` is a point on the line.

We are given in the problem that
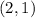`(2, 1)` is a point on the line, so we can identify the following variables to plug into point-slope form:

• 
  `a = 2`
• 
  `b = 1`

We know that a slope that is perpendicular to a given slope is its negative reciprocal. In equation form:

`m_\perp = -(1)/(m)`

We can find this for
`m = -1/3` :

`m_\perp = -\frac{\text{ }1\text{ }}{-(1)/(3)}`

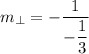
↓ skip, flip, and multiply

`m_\perp = -1 \cdot \left(-\frac{3}1\right)`

`m_\perp = 3`

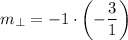
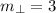
Now that we have
`a`,
`b`, and
`m`, we can find an equation for the line perpendicular to
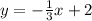`y=-(1)/(3)x + 2` that goes through
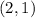`(2, 1)` by plugging these values into the point-slope form equation:

`y - b = m_\perp(x - a)`

`y - 1 = 3(x - 2)`

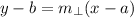
Finally, we can convert this to slope-intercept form by isolating
`y`.

`y - 1 = 3(x - 2)`

↓ apply the distributive property to the right side ...
`a(b + c) = ab + ac`

`y - 1 = 3x - 6`

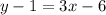
↓ add 1 to both sides

`\boxed{y = 3x - 5}`