Question

For the reaction: 2 A (g) + B (s)

= 2 C(s) + D (g)
At 298 K in a 10.0 L vessel, the
equilibrium values are as follows:
0.721 atm of A, 4.18 mol of B,
6.25 mol of C, and 4.36 atm of D.
What is the value of the
equilibrium constant?

Answer 1

Answer: The value of the equilibrium constant is K = 191.

Step-by-step explanation:

We are given the reaction:

`2 \ \text{A (g)} + \text{B (s)} \rightleftharpoons 2 \ \text{C (s)} + \text{D (g)}`

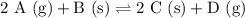
To determine the equilibrium constant, we need the concentrations of each substance at equilibrium.

We can easily determine the concentrations of the solid substances:

`[B] = 4.18 \text{ mol} / 10.0 \text{ L} = 0.418 \text{ M}`

`[C] = 6.25 \text{ mol} / 10.0 \text{ L} = 0.625 \text{ M}`

For the gaseous substances, we need to convert the given pressures into number of moles. This can be done using the Ideal Gas Law:

`PV = nRT`

or, rearranged for the number of moles:

`n = (PV)/(RT)`

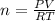
We will use the gas constant value of
`R = 0.08206 \text{ L atm mol}^(-1) \text{ K}^(-1)`.

Then, we have:

`n_A = \frac{(0.721 \text{ atm})(10.0 \text{ L})}{(0.08206 \text{ L atm mol}^(-1) \text{ K}^(-1))(298 \text{ K})} = 0.295 \text{ mol}`

`n_D = \frac{(4.36 \text{ atm})(10.0 \text{ L})}{(0.08206 \text{ L atm mol}^(-1) \text{ K}^(-1))(298 \text{ K})} = 1.78 \text{ mol}`

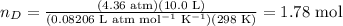
Using our newly found number of moles, we can calculate the concentrations of the gaseous substances:

`[A] = 0.295 \text{ mol} / 10.0 \text{ L} = 0.0295 \text{ M}`

`[D] = 1.78 \text{ mol}/10.0 \text{ L} = 0.178 \text{ M}`

Finally, taking everything together, and paying attention to our chemical reaction coefficients, we calculate the equilibrium constant:

`K_c = ([C]^2[D])/([A]^2[B]) = ((0.625)^2(0.178))/((0.0295)^2(0.418)) = 191`