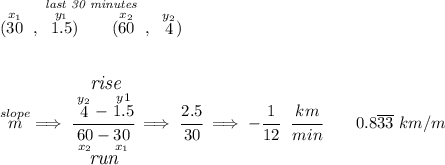Question

This distance-time graph represents a journey made by Jo

a) At what speed was Jo walking for the first 15 minutes?
b) At what speed was Jo walking for the last 30 minutes?

Answer 1

the slope goes by several names

• average rate of change

• rate of change

• deltaY over deltaX

• Δy over Δx

• rise over run

• gradient

• constant of proportionality

however, is the same cat wearing different costumes.

so the speed in this case will be the rate of change or namely the slope, hmm to get the slope of any straight line, we simply need two points off of it, let's use those two in the picture below for both intervals

`\stackrel{ \textit{first 15 minutes} }{(\stackrel{x_1}{0}~,~\stackrel{y_1}{0})\qquad (\stackrel{x_2}{15}~,~\stackrel{y_2}{1})} \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{1}-\stackrel{y1}{0}}}{\underset{\textit{\large run}} {\underset{x_2}{15}-\underset{x_1}{0}}} \implies \cfrac{ 1 }{ 15 } \implies \cfrac{1}{15} ~~ \cfrac{km}{min}\qquad 0.0\overline{66}~km/m \\\\[-0.35em] ~\dotfill`

`\stackrel{ \textit{last 30 minutes} }{(\stackrel{x_1}{30}~,~\stackrel{y_1}{1.5})\qquad (\stackrel{x_2}{60}~,~\stackrel{y_2}{4})} \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{\textit{\large rise}} {\stackrel{y_2}{4}-\stackrel{y1}{1.5}}}{\underset{\textit{\large run}} {\underset{x_2}{60}-\underset{x_1}{30}}} \implies \cfrac{ 2.5 }{ 30 } \implies - \cfrac{1}{12} ~~ \cfrac{km}{min}\qquad 0.8\overline{33}~km/m`

Answer 2

a) 1/15 or 0.067 km/s

b) 2.5/30 or 0.083 km/s

Step-by-step explanation: To calculate the speed, you would need to find the slope of the distance vs. time graph. To do this, simply divide the change in distance over the change in time. For example, for the first 15 minutes, it would be 1 divided by 15 since Jo's change in distance was 1 km and the change in time was 15 minutes.