Question

12 points if someone gets it right.

You randomly draw twice from this deck of cards. What is the probability of drawing a 7, then drawing a prime number, replacing the first card? write you answer as a fraction.

Numbers: 7 6 4 9 4 7 9

Answer 1

`(1)/(21)`

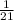
Explanation:

I don't understand what it means to replace the

first card in this example, but I solved it as if you draw a 7 and then a prime number.

First of all, the only prime number from 4, 6, 7 and 9 is 7.

That means that basically you have to draw the two 7s.

Since you don't put the first card back it's:

`\frac{ \binom{2}{2} }{ \binom{7}{2} } = (1)/(21)`

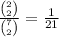
at the top it's the favorable outcome, that you draw the two 7s, and at the bottom is all the options (that you draw two cards out of seven)

You can also do it like this:

`(1)/(7) * (1)/(6) * 2 = (1)/(21)`

here the 1/7 is that you draw one 7 out of the seven cards, and the 1/6 is that you draw the second 7 out if the now six cards (because you've already drawn one). But then you have to multiply it by 2, because it doesn't matter which 7 you draw first.

I hope I got the task right, but sorry if I messed up because English isn't my first language!