Question

PLEASE HELP! 100 POINTS!

Answer 1

`n=85e^(0.0335t)`

3:22 PM

Explanation:

To write an exponential growth equation to represent the number n of cells in the dish after t minutes, we can use the exponential function formula:

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function with base $e$}\\\\$y=ae^(kx)$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $e$ is Euler's number. \\ \phantom{ww}$\bullet$ $k$ is some constant.\\\phantom{ww}$\bullet$ $x$ is the independent variable.\\\phantom{ww}$\bullet$ $y$ is the dependant variable\\\end{minipage}}`

Let the number of bacteria at 1:00 PM be the initial value, so a = 85.

The number of minutes, t, is the independent variable, so x = t.

The number of cells, n, is the dependent variable, so y = n.

Substituting these values into the formula, we get:

`\boxed{n=85e^(kt)}`

where:

• n is the number of bacteria cells.
• t is the time (in minutes) after 1:00 PM.

We are told that after 75 minutes, the number of bacteria is 1050.

Therefore, when t = 75, n = 1050.

Substitute these values into the equation and solve for k:

`1050=85e^(75k)`

`e^(75k)=(1050)/(85)`

`\ln e^(75k)=\ln \left((1050)/(85)\right)`

`75k=\ln \left((1050)/(85)\right)`

`k=(1)/(75)\ln \left((1050)/(85)\right)`

`k=0.0335185891...`

`k=0.0335\; \sf (3\;s.f.)`

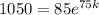
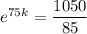
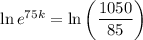
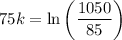
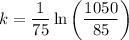
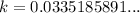
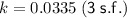
Therefore, the exponential growth equation to represent the number n of cells in the dish after t minutes is:

`\boxed{n=85e^(0.0335t)}`

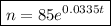
where:

• n is the number of bacteria cells.
• t is the time (in minutes) after 1:00 PM.

To predict the number of minutes after 1:00 PM when there will be 10,000 bacteria, substitute n = 10000 into the equation and solve for t:

`10000=85e^(0.0335t)`

`(10000)/(85)=e^(0.0335t)`

`\ln e^(0.0335t)=\ln \left((10000)/(85)\right)`

`0.0335t=\ln \left((10000)/(85)\right)`

`t=(1)/(0.0335)\ln \left((10000)/(85)\right)`

`t=142.319078...`

`t=142\; \sf minutes`

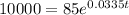
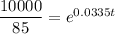
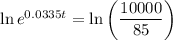
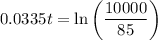
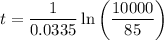
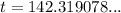
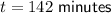
To calculate the time, add 142 minutes to 1:00 PM.

`\sf \textsf{1:00} \; PM + 142 \;minutes = \textsf{3:22} \;PM`

Therefore, the time when there will be 10,000 cells in the dish is 3:22 PM.