Question

Express cos (P+Q) in terms of trigonometric ratios of P and Q

Hence ,derive a formula ,which expresses cos 2P in terms of cos P

Answer 1

`\cos(2\text{P}) = \cos^2\text{P} - \sin^2\text{P}\\\cos(2\text{P}) = 1 - 2\sin^2\text{P}\\\cos(2\text{P}) = 2\cos^2\text{P} - 1`

Explanation:

One of the trigonometric identities is the identity of addition:

`\cos\left(\alpha + \beta\right) = \cos\alpha\cos\beta - \sin\alpha\sin\beta`

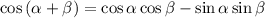
In the case where α = β, we get a new identity, which is commonly known as the double angle identity.

`\cos(2\alpha) = \cos(\alpha + \alpha) = \cos\alpha\cos\alpha - \sin\alpha\sin\alpha\\\to \cos(2\alpha) = \cos^2\alpha - \sin^2\alpha`

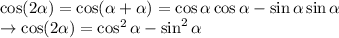
From here, we can also use the identity
`\cos^2\alpha + \sin^2\alpha = 1`.

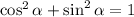If we solve for cosine squared, we get:
`cos^2\alpha = 1 - \sin^2\alpha`.
Substituting this value into the identity:

`\cos(2\alpha) = 1 - \sin^2\alpha - \sin^2\alpha = 1 - 2\sin^2\alpha`

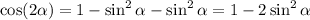
If we solve for sine squared, we get:
`\sin^2\alpha = 1-\cos^2\alpha`.
Substituting this value into the identity:

`\cos(2\alpha) = \cos^2\alpha - (1 - \cos^2\alpha) = \cos^2\alpha - 1 + \cos^2\alpha= 2\cos^2\alpha - 1`

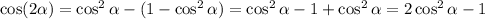
Therefore, we have three formulas for cos2P:

`\cos(2\text{P}) = \cos^2\text{P} - \sin^2\text{P}\\\cos(2\text{P}) = 1 - 2\sin^2\text{P}\\\cos(2\text{P}) = 2\cos^2\text{P} - 1`