Question

How do u doo thiss?? :)​

Answer 1

Answer: a = 5

b = -33

Explanation:

They want you to put the quadratic in vertex form. You need to complete the square to do this.

x² + 10x - 8 >Make space to complete square

x² + 10x - 8 >Take middle term 10, divide by 2 then square

that
`((10)/(2)) ^(2) = 25`

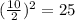
Use +25 to fill in to complete the square but you

can't just add 25 to an equation, it changes it.

You need to counterbalance it by also

subtract 25. so 25-25= 0 you are not changing

x² + 10x +25 - 8 -25 >Combine the -8 and -25

x² + 10x +25 - 33 >Factor the first 3 terms x² + 10x +25

(x+5)(x+5) -33 >(x+5)(x+5) = (x+5)²

(x+5)² - 33 >this is the form they wanted.

a = 5

b = -33

Answer 2

`\sf (x + a)^2 + b = x^2 + 10x - 8 \\`

Comparing coefficients, we can equate the corresponding terms:

`\sf 2ax = 10x \\` (coefficient of x terms)

`\sf a^2 + b = -8 \\` (constant term)

From the first equation, we can determine the value of
`\sf a \\`:

`\sf 2ax = 10x \\`

`\sf 2a = 10 \\` (canceling out x from both sides)

`\sf a = (10)/(2) \\`

Simplifying further:

`\sf a = 5 \\`

Now, we can substitute the value of
`\sf a \\` into the second equation:

`\sf a^2 + b = -8 \\`

`\sf 5^2 + b = -8 \\`

`\sf 25 + b = -8`

Solving for
`\sf b \\`:

`\sf b = -8 - 25 \\`

`\sf b = -33 \\`

Therefore, the values of
`\sf a \\` and
`\sf b \\` are
`\sf 5 \\` and
`\sf -33 \\`, respectively.

Thus, the expression
`\sf x^2 + 10x - 8 \\` can be written in the form
`\sf (x + 5)^2 - 33 \\`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`