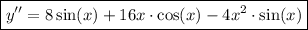Question

Find the second derivative of y= 4x^2sinx​

Answer 1

`y'' = 8\sin(x) + 16x\cdot \cos(x) - 4x^2 \cdot \sin(x)`

Explanation:

Given the function:

`y=4x^2 \cdot \sin(x)`

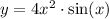
We can find its derivative, or instantaneous slope, by applying the power rule and using the common derivative of the trigonometric function sine within the product rule.

Here are the relevant formulas:

• product rule:
  `\left(\frac{}{} f(x) \cdot g(x) \frac{}{} \right)' = f(x)\cdot g'(x) + g(x) \cdot f'(x)`
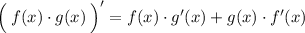
• power rule:
  `(x^a)' = ax^(a\, - \, 1)`
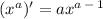
• derivative of sine:
  `(\sin(x))' = \cos(x)`

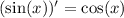
First, we can find the derivative of each of the function's factors [ which I will label
`f(x)` and
`g(x)` ].

`f(x) = 4x^2`

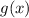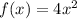
↓ applying the power rule
`(x^a)' = ax^(a\, - \, 1)`

`f'(x) = 4(2x^(2-1))`

`\bold{f'(x) = 8x}`

⎯⎯⎯⎯⎯⎯⎯

`g(x) = \sin(x)`

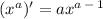
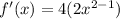
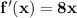
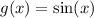
↓ applying the common derivative
`(\sin(x))' = \cos(x)`

`\bold{g'(x) = \cos(x)}`

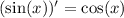
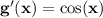
Now, we can apply the product rule using these values of
`f'(x)` and
`g'(x)`.

`\left(\frac{}{} f(x) \cdot g(x) \frac{}{} \right)' = f(x)\cdot g'(x) + g(x) \cdot f'(x)`

`y' = 4x^2 \cdot \cos(x) + \sin(x) \cdot 8x`

`\boxed{y' = 4x^2 \cdot \cos(x) + 8x \cdot \sin(x)}`

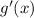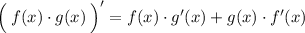
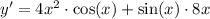
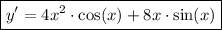
To find the second derivative of the function, we have to take the derivative of the derivative. We can apply the same concepts from the previous step, but also with the sum/difference rule.

• sum/difference rule:
  `\left(\frac{}{}f(x) \pm g(x)\frac{}{}\right)' = f'(x) \pm g'(x)`
• derivative of cosine:
  `(\cos(x))' = -\sin(x)`

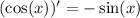
↓ applying the sum/difference rule to the function's derivative

`y'' = \left(\frac{}{}4x^2 \cdot \cos(x)\frac{}{}\right)' + \left(\frac{}{}8x \cdot \sin(x)\frac{}{}\right)'`

↓ applying the product rule to each derivative

`y'' = \left(\frac{}{} 4x^2 \cdot (-\sin(x)) + \cos(x) \cdot 8x \frac{}{}\right) + \left(\frac{}{} 8x \cdot \cos(x) + \sin(x) \cdot 8 \frac{}{}\right)`

↓ combining like terms

`\boxed{y'' = 8\sin(x) + 16x\cdot \cos(x) - 4x^2 \cdot \sin(x)}`