Question

If Julian walks from his house to his school at a speed of 3 miles per hour he will be five minutes late for class. If he cycles to school at a speed of 10 miles per hour, he will be 16 minutes early for class. Find the distance from his house to his school. *Please help as quickly as possible, this is due today.*

Answer 1

The distance to the school is 3/2 miles

Explanation:

At a speed of 3 miles per hour, he will be five minutes late for class

let t be the correct time for class,

let v be the speed of walking i.e, v = 3 miles per hour

And let w be the speed of cycling i.e, w = 10 miles per hour

(or mph)

Let the distance from his house to his school be d

In both walking and cycling, he covers the distance d in different times

t1 and t2

now, the relation between distance, time and speed is,

speed = distance/time

In the case of walking,

He arrives at the time t + 5 min since he arrives 5 min late

but since the speeds are in miles per hour, let's convert time minutes into hours,

`5 min(1 hour/60min) = 1/12 hours`

`16min(1 hour/60 min) = 4/15 \ hours`

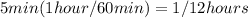
So, t1 = t + 1/12

t2 = t - 4/15

Now, for v = 3 mph, the equation will be,

`3 (mph) = (d)/(t + 1/12)\\d = 3(t + 1/12)\\d=3t+1/4`

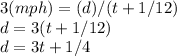
(NOTE: The hours(the unit) cancel out so we will only have miles left)

and for w = 10 mph, the equation will be,

`10 = d/(t-4/15)\\d = 10(t-4/15)\\d = 10t-8/3`

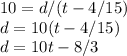
Now, we solve these 2 equations to get d

we find t,by equation these two,

`d = 3t +1/4 \\ d = 10t-8/3\\10t+8/3=3t+1/4\\\\10t-3t=1/4+8/3\\7t=35/12\\t=5/12`,

Using value of t in any of the two equations to find d,

d = 3t+1/4

d = 3(5/12) +1/4

d = 5/4 + 1/4

d = 6/4

d = 3/2 miles

Hence the distance to the school is 3/2 miles