Question

Nicole invests $2000 in an account. The account pays compound interest at a rate of K% per year. At the end of the first year, the money in the account is $2036. (i) Show that K = 1.8. (ii) Find the number of complete years before Nicole has at least $2150 in the account. Show full working​

Answer 1

i) See proof below.

ii) 5 years

Explanation:

To solve this problem, we can use the formula for annual compound interest:

`\boxed{\begin{minipage}{7 cm}\underline{Annual Compound Interest Formula}\\\\$ A=P\left(1+r\right)^(t)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Given values:

• A = $2036
• P = $2000
• t = 1 year

Substitute the values into the formula and solve the equation for r:

`2036=2000(1+r)^1`

`2036=2000(1+r)`

`(2036)/(2000)=1+r`

`1.018=1+r`

`r=1.018-1`

`r=0.018`

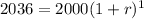
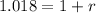
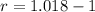
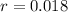
Multiply by 100 to convert to a percentage:

`r = 0.018 * 100=1.8\%`

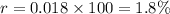
Therefore, the interest rate per year, K, is 1.8%.

To find the number of complete years before Nicole has at least $2,150 in the account, substitute A = 2150, P = 2000, and r = 0.018 into the formula, and solve for t.

`2150=2000(1+0.018)^t`

`2150=2000(1.018)^t`

`(2150)/(2000)=(1.018)^t`

`1.075=(1.018)^t`

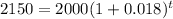
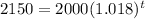
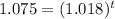
Take natural logs of both sides of the equation:

`\ln 1.075= \ln (1.018)^t`

`\textsf{Apply the log power law:} \quad \ln x^n=n \ln x`

`\ln 1.075= t \ln 1.018`

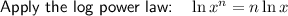
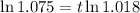
Divide both sides of the equation by ln(1.018):

`(\ln 1.075)/(\ln 1.018)= (t \ln 1.018)/(\ln 1.018)`

`t=4.05386734...`

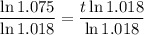
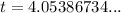
As we need to find the number of complete years before Nicole has at least $2,150 in the account, we need to round up the found value of t to the nearest complete year.

From our calculations, t ≈ 4.05 years, so the balance of the account reaches $2,150 after 4 years and during the 5th year. (After 4 years, the account balance is $2,147.93).

Therefore, the number of complete years before Nicole has at least $2,150 in the account is 5 years.