Question

I can't seem to figure out the method...​

Answer 1

Answer: C. 400g

Step-by-step explanation:

From the picture we can say that:

`(Force * length)_(left) =(Force * length)_(right)`

Assume the length is the distance from the fulcrum to the mass.

`(20cm)(200g * 980 (cm)/(s^(2)) )=(60-50cm)(m_(beam) * 980 (cm)/(s^(2)) )`

The center of mass is 50cm from the end, and the length from the end to the pivot is 60cm thus center of mass is 10 cm from the pivot.

Canceling out the acceleration due to gravity gives:

`10*m_(beam) =4000g`

`m_(beam) =400g`

Answer 2

C) 400 g

Step-by-step explanation:

To calculate the mass of the beam, first label the forces on the given diagram (attached).

An object’s weight is a force caused by gravity.

The equation for Weight (W) is:

`\boxed{W=m\text{g}}`

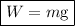
where:

• Weight (W) is a force (measured in Newtons).
• m is the mass (measured in kg).
• g is acceleration due to gravity (9.8 ms⁻²)

As 200 g = 0.2 kg, the weight of a mass of 200 g is:

`\boxed{W_(\sf mass)=0.2\text{g}}`

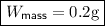
Let the mass of the beam be M kg. Therefore, the weight of the beam is:

`\boxed{W_(\sf beam)=M\text{g}}`

The centre of mass (COM) of an object is the point where the object’s weight can be considered to act. Weight always acts downwards. Therefore, add the force of 0.2g acting downwards from the mass, and the force of Mg acting downwards at 50 cm from the right-hand side of the beam.

The Normal Reaction (R) is the reaction from a surface. Reaction is always at 90° to the surface. Therefore, add the reaction force (Rₓ) of the support X to the diagram.

We can now calculate the mass of the beam by using moments.

A moment is the turning effect a force has around a point.

The formula to find the moment of a force about a point is:

`\boxed{\text{Moment}=Fd}`

where:

• F is the magnitude of force (measured in Newtons)
• d is the perpendicular distance from the line of action of the force to the pivot (in metres).

As the horizontal beam is in equilibrium, we know that clockwise moments = anticlockwise moments.

We don't know the value of the normal reaction at X, so we will take moments about X.

Taking moments about X (with clockwise being the positive direction):

`\begin{aligned}M\text{g} * 0.1\; \textsf{m} &= 0.2\text{g} * 0.2\; \textsf{m}\\0.1M &= 0.04\\M &= 0.4\end{aligned}`

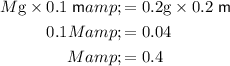
Therefore, the value of M is 0.4, so the mass of the beam is 0.4 kg, which is 400 g.