Answer:
12.72°
Explanation:
As PA = PB = PC = PD, the pyramid is a right rectangular pyramid, where its apex is above the center of the base ABCD.
Let the center of the base ABCD be point O.
Triangle POB is a right triangle (see attached diagram).
Therefore, the angle between PB and the base ABCD is angle PBO of right triangle POB (labelled "x" on the attached diagram).
We already have the hypotenuse of triangle POB: PB = 14 cm.
Therefore, to find angle PBO, we need to find the length of one of the legs of triangle POB and use a trigonometric ratio.
As the diagonals of a rectangle bisect each other, the base of the triangle POB is half the diagonal DB.
To find the length of the diagonal DB of the base ABCD, we can use Pythagoras Theorem:
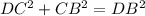
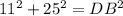
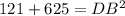
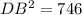

As OB is half of DB:
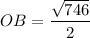
Now we have the side adjacent to angle PBO (side OB) and the hypotenuse (side PB) of right triangle POB, we can use the cosine trigonometric ratio to calculate angle PBO:
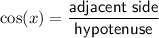
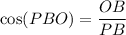
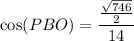
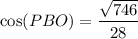

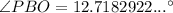

Therefore, the angle between PB and the base ABCD is 12.72°, to two decimal places.