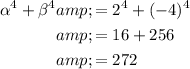Question

If a and ẞ are the zeroes of the polynomial f(x) = x ^ 2 + 2x - 8 then evaluate: α^4 + ẞ^4

Answer 1

There are at least two ways of doing that.

First one is just to find those roots: x² + 2x - 8 = x² + 2x + 1 - 9 = (x + 1)² - 3² = (x+1+3)(x+1-3) = (x+4)(x-2). α = 2; β = -4; α⁴+β⁴= 16 + 256 = 272.

The second way is a bit nore interesting, and you can easily evaluate this even if the roots are "bad" (irrational or complex, for example). What we should do now is to use Vieta's formulas: we know that α + β = -2 and αβ = -8. Now we can find that (α + β)² = (-2)² = 4 = α² + β² + 2αβ; since αβ = -8, 2αβ = -16. α² + β² - 16 = 4; α² + β² = 20; α²β² = (αβ)² = 64. (α² + β²)²= 20² = 400 = α⁴ + β⁴ + 2α²β²; 2α²β² = 128; α⁴ + β⁴ = 400 - 128 = 272. It lead us to the same answer.

Answer 2

α⁴ + β⁴ = 272

Explanation:

To find the value of α⁴ + β⁴, we can use Vieta's formulas, which relate the coefficients of a polynomial to its roots.

Vieta's formulas state that for a quadratic polynomial of the form ax² + bx + c, with roots α and β, the following relationships hold:

`\bullet \quad \textsf{Sum of the roots:} \quad \alpha + \beta=-(b)/(a)`

`\bullet \quad \textsf{Product of the roots:} \quad \alpha \beta=(c)/(a)`

For the polynomial f(x) = x² + 2x - 8, the coefficients are:

• a = 1, b = 2 and c = -8.

As f(x) has roots α and β, then according to Vieta's formulas:

`\alpha + \beta = -(2)/(1)=-2`

`\alpha \beta=(-8)/(1)=-8`

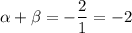
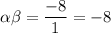
Using the identity a² + b² = (a + b)² - 2ab, we can rewrite α⁴ + β⁴ in terms of (α + β) and αβ:

`\begin{aligned}\alpha^4 + \beta^4 &= (\alpha^2)^2 + (\beta^2)^2\\&=(\alpha^2+\beta^2)^2-2\alpha^2\beta^2\\&=((\alpha + \beta)^2 - 2\alpha \beta)^2-2(\alpha\beta)^2\end{aligned}`

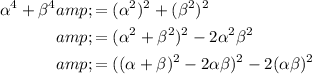
Substitute the values of (α + β) = -2 and αβ = -8:

`\begin{aligned}\alpha^4 + \beta^4 &=((-2)^2 - 2(-8))^2-2(-8)^2\\&=(4+16)^2-2(64)\\&=(20)^2-128\\&=400-128\\&=272\end{aligned}`

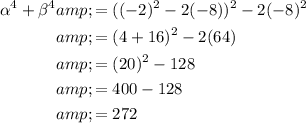
Therefore, α⁴ + β⁴ = 272.

`\hrulefill`

The other method we can use is to find the zeroes of the polynomial by factoring the quadratic:

`\begin{aligned}f(x)&=x^2+2x-8&\\&=x^2+4x-2x-8\\&=x(x+4)-2(x+4)\\&=(x-2)(x+4)\end{aligned}`

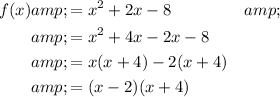
Set the factored quadratic to zero, and solve for x:

`\begin{aligned}(x-2)(x+4)&=0\\\\x-2&=0 \implies x=2\\x+4&=0 \implies x=-4\end{aligned}`

Therefore, the zeroes of the polynomial are 2 and -4.

If α and β are the zeroes, then α = 2 and β = -4. Therefore:

`\begin{aligned}\alpha^4+\beta^4&=2^4+(-4)^4\\&=16+256\\& = 272\end{aligned}`