Question

The Sum of an A.P is 20, the first term being 8, what is the common difference and number of terms ?​

Answer 1

The common difference d = 0 and the number of terms n = 4.

Step-by-step explanation

We know that the sum S of the first n terms of an arithmetic progression (A.P) is given by the formula:

`S = (n)/(2) * [2a + (n-1)d]`

where a is the first term, d is the common difference, and n is the number of terms.

In this problem, we are given that S = 20 and a = 8. We need to find d and n.

Substituting the given values in the formula, we get:

`20 = (n)/(2) * [2(8) + (n-1)d]`

Simplifying the equation, we get:

`20 = 4n + (n-1)d`

`20 = 5n - d`

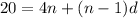
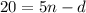
We can rewrite this equation as:

`d = 5n - 20`

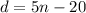
Now, we also know that the first term of the A.P is 8. Using this and the formula for the nth term of an A.P, we get:

`a + (n-1)d = 8\\`

Substituting the value of d from earlier, we get:

`8 + (n-1)(5n-20) = 0`

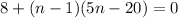
Simplifying this quadratic equation, we get:

`5n^2 - 15n - 8 = 0`

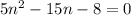
Using the quadratic formula, we get:

n = (15 ± √385) / 10

Since n must be a positive integer, we can take the value of n as:

n = (15 + √385) / 10

n ≈ 3.84

Therefore, the number of terms should be rounded up to the nearest integer, which is 4.

Now that we know n = 4, we can substitute it back into the equation for d:

`d = 5n - 20`

`d = 5(4) - 20`

`d = 0`

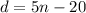
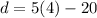
Therefore, the common difference is 0, which means that all the terms in the A.P are the same. In this case, since there are 4 terms, each term must be:

8 / 4 = 2

Therefore, the common difference d = 0 and the number of terms n = 4.