Question

Please solve this question it’s urgently due tomorrow !!!!!!

Answer 1

∠BEC = 56.13°

Explanation:

Triangle CBE is a right triangle, where angle CBE is 90°. The legs of triangle CBE are line segments CB and BE. The hypotenuse of triangle CBE is EC. (Refer to the attached diagram).

To find the angle BEC (labelled "x" on the attached diagram), we can use a trigonometric ratio, but as we only know one side length of the triangle (BC = 22 cm), we first need to find another side length.

(As BE is the diagonal of rectangle ABFE, it is much simpler to find the length of BE rather than the space diagonal EC).

As parallel edges of a rectangular prism are congruent, BF = 13 cm and EF = 7 cm. Therefore, we can therefore use Pythagoras Theorem to find the length of BE.

`BF^2+EF^2= BE^2`

`13^2+7^2= BE^2`

`169+49= BE^2`

`BE^2=218`

`BE=√(218)\; \sf cm`

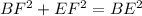
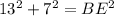
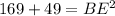
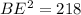
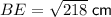
Now we know the lengths of the side opposite angle BEC (side BC) and the side adjacent to angle BEC (side BE), we can use the tangent trigonometric ratio to calculate angle BEC:

`\tan(x)=\sf (opposite\;side)/(adjacent\;side)`

`\tan(BEC)=(BC)/(BE)`

`\tan(BEC)= (22)/(√(218))`

`\angle BEC=\tan^(-1)\left( (22)/(√(218))\right)`

`\angle BEC=56.1333193...^(\circ)`

`\angle BEC=56.13^(\circ)\; \sf (2\;d.p.)`

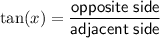
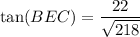
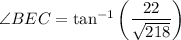
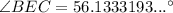
Therefore, angle BEC is 56.13° to two decimal places.