Question

What are all the real and complex solutions of the equation x³ + 5x² + 5x = 0? Select all that apply. Hint: Factor, then use quadratic formula.

Answer 1

Explanation:

First, we can factor out an x from each term in the equation:

x(x² + 5x + 5) = 0

Setting each factor equal to zero gives two equations:

x = 0

x² + 5x + 5 = 0

The solution to the first equation is x = 0, which is a real number.

The solution to the second equation can be found using the quadratic formula:

`x=\frac{-b+ \sqrt{b^(2) -4ac}}{2a}`

`x=\frac{-b- \sqrt{b^(2) -4ac}}{2a}`

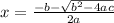
For the equation x² + 5x + 5 = 0, we have a = 1, b = 5, and c = 5.

Plugging these into the quadratic formula gives:

`x = \frac{-5+\sqrt{5^(2) -4 (1)(5)}}{2(1)}`

`x=(-5+√(25-20))/(2)`

`x= (-5+√(5) )/(2) ,x= (-5-√(5) )/(2)`

`x=(-5)/(2)+ (√(5))/(2) ,x= (-5)/(2)- (√(5))/(2)`

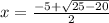
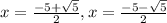
So the solutions are:

`x = 0`

`x=(-5)/(2)+ (√(5))/(2)`

`x= (-5)/(2)- (√(5))/(2)`

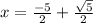
All solutions in this case are real. There are no complex solutions because the discriminant (b² - 4ac) of the quadratic equation is greater than 0, which means there are two distinct real roots for the quadratic part of the equation.