Question

I proceed to calculate the degree of angles and lengths of angle FBE but I'm not sure how to calculate the length of DF

Answer 1

B. 15 cm

Explanation:

Answer 2

B = 15 cm

Explanation:

As BE is an extension of AB, and ABCD is a square (so its interior angles are all right angles), triangle EBF is a right triangle.

If BE = 4 cm and EF = 5 cm, we can use Pythagoras Theorem to calculate the length of BF:

`BF^2+BE^2=EF^2`

`BF^2+4^2=5^2`

`BF^2+16=25`

`BF^2=9`

`BF=3\;\sf cm`

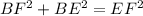
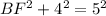
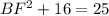
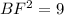
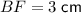
As BE is an extension of AB, and ABCD is a square, then BE is parallel to CD. This means that the interior angles of triangle EBF are equal to the corresponding interior angles of triangle DCF. Therefore, the two triangles are similar: ΔEBF ~ ΔDCF.

In similar triangles, corresponding sides are always in the same ratio:

BE : CD = BF : CF = EF : DF

Let "x" be the side length of the square. Therefore:

• CD = x
• CF = (x - 3)

Substitute these into the ratio and solve for x:

`\begin{aligned}\sf BE: CD&=\sf BF : CF\\\\4 : x &= 3: (x - 3)\\\\(4)/(x)&=(3)/((x-3))\\\\4(x-3)&=3x\\\\4x-12&=3x\\\\4x-12-3x&=3x-3x\\\\x-12&=0\\\\x-12+12&=0+12\\\\x&=12\end{aligned}`

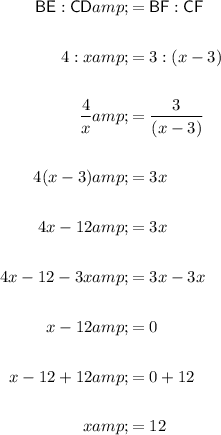
Therefore:

• CD = x = 12 cm
• CF = x - 3 = 9 cm

Substitute these values back into the ratio equation and solve for DF:

`\sf BE: CD = BF : CF = EF : DF\\\\\phantom{w}4 : 12 \;\:= \;\:\:3 : 9 \;\;= \;\;\:5 : \sf DF`

Therefore:

`(3)/(9)=(5)/(\sf DF)`

`3 \;\textsf{DF}=45`

`\textsf{DF}=(45)/(3)`

`\textsf{DF}=15\; \sf cm`

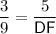
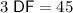
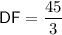
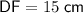
Therefore, the length of DF is 15 cm.