Question

NO LINKS!! URGENT HELP PLEASE!!

Find the value of x

Answer 1

84

Explanation:

When a tangent and a secant, two secants, or two tangents intersect outside a circle then the measure of the angle formed is one-half the positive difference of the measures of the intercepted arcs.

31 = 1/2 (146 - x)

62 = 146 - x

x = 146 - 62 = 84

Answer 2

x = 84

Explanation:

A secant is a straight line that intersects a circle at two points.

The given diagram shows a circle with two secants drawn to the circle from one exterior point.

To find the value of x, we can use the Intersecting Secants Theorem.

Intersecting Secants Theorem

If two secant segments are drawn to the circle from one exterior point, the measure of the angle formed by the two lines is half of the (positive) difference of the measures of the intercepted arcs.

From inspection of the given diagram:

• The angle formed by the two secants is 31°.
• The two intercepted arcs are 146° and x°.

Therefore, according to the Intersecting Secants Theorem:

`31^(\circ)=(1)/(2)\left(146^(\circ)-x^(\circ)\right)`

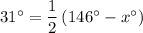
Solving the equation for x:

`62^(\circ)=146^(\circ)-x^(\circ)`

`x^(\circ)=146^(\circ)-62^(\circ)`

`x^(\circ)=84^(\circ)`

`x=84`

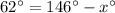
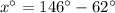
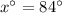
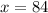
Therefore, the value of x is 84.