Answer:
The first six terms of the sequence
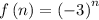 are:
are:

Explanation:
Given the sequence
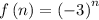
Here
 represents any term number in the sequence
represents any term number in the sequence
Determining the first term
substitute n = 1 in the sequence to determine the first term
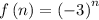
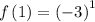

Thus, the first term is -3.
Determining the 2nd term
substitute n = 2 in the sequence to determine the 2nd term
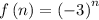
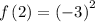
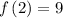
Thus, the 2nd term is 9.
Determining the 3rd term
substitute n = 3 in the sequence to determine the 3rd term
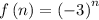
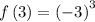
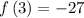
Thus, the 3rd term is -27.
Determining the 4th term
substitute n = 4 in the sequence to determine the 4th term
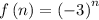
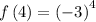
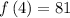
Thus, the 4th term is 81.
Determining the 5th term
substitute n = 5 in the sequence to determine the 5th term
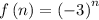
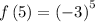
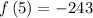
Thus, the 5th term is -243.
Determining the 6th term
substitute n = 6 in the sequence to determine the 6th term
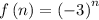
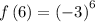
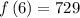
Thus, the 6th term is 729
Therefore, the first six terms of the sequence
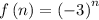 are:
are:
