Question

The surface area of the pyramid shown rounded to the nearest whole number is __ m^2

Answer 1

To the nearest whole number, the surface area is,

SA = 866 m^2

Explanation:

We see that all the side lengths of the base are 10m

Similarly the height of the triangles is 13m

So, since there are 6 triangles, with base 10 and height 13,

we use the formula for area of a triangle,

A = (1/2)(base)(height)

A = (1/2)(10)(13)

A = (5)(13)

A = 65

and since there are 6 triangles, we surface area due to the triangles is

(6)(65) = 390 m^2 = area due to 6 triangles = B

Now,

We have to calculate the area of the base,

The length of the apothem is given as

`6√(7)`

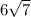
So, using the formula for hexagon Area, H = 3sa, with side length 10m and apothem

`6√(7)`

`H = 3(10)(6√(7) )= 180√(7)`

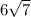
so the total surface area would be,

SA = B + H

`SA = (390) + (180√(7) )\\SA = 390 + 476.235\\SA = 866.235`

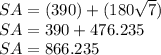
To the nearest whole number, the surface area is,

SA = 866 m^2