Question

Find the variance of the data.
251, 224, 237, 255, 268
X = 247
Variance (0²) = [?]

Answer 1

Variance (σ²) = 230

Explanation:

Variance is a way to measure how spread out or varied a set of numbers is from the mean. It is calculated by subtracting the mean from each data point, squaring the result, and then taking the average of those squared differences.

Given data set:

• 251, 224, 237, 255, 268

To find the variance of a set of data, we first need to calculate the mean of the data by dividing the sum of the data points by the number of data points:

`\textsf{Mean $(\overline{x})$}=(251+224+237+255+268)/(5)=(1235)/(5)=247`

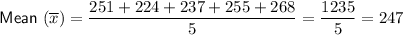
Subtract the found mean from each data point, and square the result:

`(251 - 247)^2 = 4^2=16`

`(224 - 247)^2 = (-23)^2=529`

`(237 - 247)^2 = (-10)^2=100`

`(255 - 247)^2 = 8^2=64`

`(268 - 247)^2 = 21^2=441`

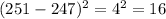
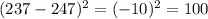
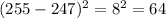
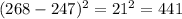
The variance of the data is the mean of the squared differences:

`\textsf{Variance $(\sigma^2)$} = (16 + 529 + 100 + 64 + 441)/(5)=(1150)/(5)=230`

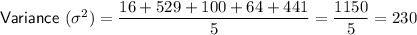
Therefore, the variance of the given data set is 230.