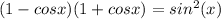Question

Simplify (1-cos x)(1+cos x)

Answer 1

To simplify the expression
`\sf\:(1-\cos x)(1+\cos x)\\`, follow these steps:

Step 1: Apply the distributive property.

`\longrightarrow\sf\:(1-\cos x)(1+\cos x) = 1 \cdot 1 + 1 \cdot \\`
`\sf\: \cos x -\cos x \cdot 1 - \cos x \cdot \cos x\\`

Step 2: Simplify the terms.

`\longrightarrow\sf\:1 + \cos x - \cos x - \cos^2 x\\`

Step 3: Combine like terms.

`\longrightarrow\sf\:1 - \cos^2 x\\`

Step 4: Apply the identity
`\sf\:\cos^2 x = 1 - \sin^2 x\\`.

`\sf\:1 - (1 - \sin^2 x)\\`

Step 5: Simplify further.

`\longrightarrow\sf\:1 - 1 + \sin^2 x\\`

Step 6: Final result.

`\sf\red\bigstar{\boxed{\sin^2 x}}\\`

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`

Answer 2

`sin^2x`

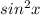
Explanation:

To simplify the expression (1 - cos x)(1 + cos x), we can use the difference of squares identity, which states that
`a^2 - b^2 = (a + b)(a - b).`

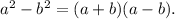
Let's apply this identity to the given expression:

`(1 - cos x)(1 + cos x) = 1^2 - (cos x)^2`

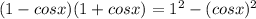
Now, we can simplify further by using the trigonometric identity
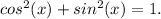`cos^2(x) + sin^2(x) = 1.` By rearranging this identity, we have
`cos^2(x) = 1 - sin^2(x).`

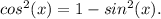
Substituting this into our expression, we get:

`1^2 - (cos x)^2 = 1 - (1 - sin^2(x))`

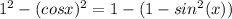
Simplifying further:

`1 - (1 - sin^2(x)) = 1 - 1 + sin^2(x)`

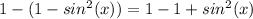
Finally, we get the simplified expression:

`(1 - cos x)(1 + cos x) = sin^2(x)`