Assume
![\sf\:f : [a, b] \rightarrow \mathbb{R} \\](https://img.qammunity.org/2024/formulas/mathematics/high-school/jpv5cfeubgfhowxr2ai8b2hsavskj8pjw4.png) is integrable. We want to show that if
is integrable. We want to show that if
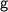 satisfies
satisfies
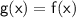 for all but a finite number of points in
for all but a finite number of points in
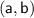 , then
, then
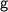 is integrable as well and
is integrable as well and
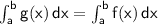 .
.
Proof:
Assume there exists a point
 in
in
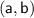 where
where
 and
and
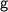 differ.
differ.
Since
 is integrable, by definition, for any given
is integrable, by definition, for any given
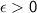 , there exists a partition
, there exists a partition
 of
of
![\sf\:[a, b]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bwtwlr3o1a8fbb3suj28pcukhjpepf0jcd.png) such that the upper sum
such that the upper sum
 .
.
Let's consider the partition
 which includes the point
which includes the point
 . Without loss of generality, assume
. Without loss of generality, assume
 is the right endpoint of a subinterval
is the right endpoint of a subinterval
![\sf\:[x_i, x_(i+1)] \\](https://img.qammunity.org/2024/formulas/mathematics/high-school/bjojns92cbpphvkyqlsxkueto8053ygu1c.png) in
in
 .
.
Since
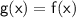 for all but a finite number of points, we can select a subinterval
for all but a finite number of points, we can select a subinterval
![\sf\:[x_i, x_(i+1)] \\](https://img.qammunity.org/2024/formulas/mathematics/high-school/bjojns92cbpphvkyqlsxkueto8053ygu1c.png) such that
such that
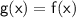 for all
for all
 in
in
![\sf\:[x_i, x_(i+1)] \\](https://img.qammunity.org/2024/formulas/mathematics/high-school/bjojns92cbpphvkyqlsxkueto8053ygu1c.png) except
except
 .
.
Now, we have:
![\sf\:\sup_{x \in [x_i, x_(i+1)]} g(x) - \inf_{x \in [x_i, x_(i+1)]} g(x) = \sup_{x \in [x_i, x_(i+1)]} f(x) - \inf_{x \in [x_i, x_(i+1)]} f(x) \\](https://img.qammunity.org/2024/formulas/mathematics/high-school/k6gcw8p6lxhxnosfah6o7z19u4ryike26s.png)
Using this, we can rewrite the upper sum and lower sum as:
![\sf\:U(g, P) = U(f, P) + \sup_{x \in [x_i, x_(i+1)]} g(x) - \inf_{x \in [x_i, x_(i+1)]} g(x) \\](https://img.qammunity.org/2024/formulas/mathematics/high-school/ek6qopfvtgrjwkbu6oxaxi4tl2gjj2cqp2.png)
![\sf\:L(g, P) = L(f, P) + \sup_{x \in [x_i, x_(i+1)]} g(x) - \inf_{x \in [x_i, x_(i+1)]} g(x) \\](https://img.qammunity.org/2024/formulas/mathematics/high-school/trijvxmy5gheza3r5ylgw760po10si17qw.png)
Since
 is integrable, we have
is integrable, we have
 . Therefore,
. Therefore,
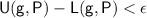 as well.
as well.
This holds for any partition
 of
of
![\sf\:[a, b]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bwtwlr3o1a8fbb3suj28pcukhjpepf0jcd.png) . Hence,
. Hence,
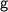 is integrable and
is integrable and
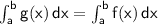 .
.