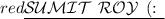Given information: $\sf\:\csc(x) = 8$, $90° < x < 180° \\$
To find $\sf\:\sin(\frac{x}{2}) \\$, $\sf\:\cos(\frac{x}{2}) \\$, and $\sf\:\tan(\frac{x}{2}) \\$:
Step 1: Rewrite the given information:
$\sf\:\csc(x) = \frac{1}{\sin(x)} = 8 \\$
Step 2: Solve for $\sf\:\sin(x) \\$:
$\sf\:\sin(x) = \frac{1}{8} \\$
Step 3: Use the half-angle identity for $\sf\:\sin(\frac{x}{2}) \\$:
$\sf\:\sin(\frac{x}{2}) = \pm \sqrt{\frac{1 - \cos(x)}{2}} \\$
Since $\sf\:90° < x < 180°$, $\sf\:\cos(x)$ will be negative, so we take the positive square root:
$\sf\:\sin(\frac{x}{2}) = \sqrt{\frac{1 - \cos(x)}{2}} \\$
Step 4: Find $\sf\:\cos(x)$ using the Pythagorean identity:
$\sf\:\sin^2(x) + \cos^2(x) = 1 \\$
Substituting $\sf\:\sin(x) = \frac{1}{8} \\$:
$\sf\:(\frac{1}{8})^2 + \cos^2(x) = 1 \\$
$\sf\:\frac{1}{64} + \cos^2(x) = 1 \\$
$\sf\:\cos^2(x) = 1 - \frac{1}{64} \\$
$\sf\:\cos^2(x) = \frac{63}{64} \\$
Taking the square root of both sides:
$\sf\:\cos(x) = \pm \sqrt{\frac{63}{64}} \\$
Since $\sf\:90° < x < 180°$, $\sf\:\cos(x)$ will be negative, so we take the negative square root:
$\sf\:\cos(x) = -\sqrt{\frac{63}{64}} \\$
Step 5: Use the half-angle identity for $\sf\:\cos(\frac{x}{2})$:
$\sf\:\cos(\frac{x}{2}) = \pm \sqrt{\frac{1 + \cos(x)}{2}} \\$
Since $\sf\:90° < x < 180°$, $\sf\:\cos(x)$ will be negative, so we take the negative square root:
$\sf\:\cos(\frac{x}{2}) = -\sqrt{\frac{1 + \cos(x)}{2}} \\$
Step 6: Find $\sf\:\tan(\frac{x}{2}) \\$ using the identity $\sf\:\tan(\frac{x}{2}) = \frac{\sin(\frac{x}{2})}{\cos(\frac{x}{2})} \\$:
$\sf\:\tan(\frac{x}{2}) = \frac{\sqrt{\frac{1 - \cos(x)}{2}}}{-\sqrt{\frac{1 + \cos(x)}{2}}} \\$
Simplifying:
$\sf\:\tan(\frac{x}{2}) = -\sqrt{\frac{1 - \cos(x)}{1 + \cos(x)}} \\$
Therefore, the values are:
$\sf\:\sin(\frac{x}{2}) = \sqrt{\frac{1 - \cos(x)}{2}} \\$
$\sf\:\cos(\frac{x}{2}) = -\sqrt{\frac{1 + \cos(x)}{2}} \\$
$\sf\:\tan(\frac{x}{2}) = -\sqrt{\frac{1 - \cos(x)}{1 + \cos(x)}} \\$
Please note that the sign of the values may change depending on the actual value of $\sf\:\cos(x)$, which is negative in this case.
♥️