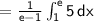Question

Simplify the following expression. + dp d | dx p2 5 교 + d dp || dx pi 5 Use symmetry to evaluate the following integral. 9 (1+x+x2 + x®) dx ? -9 9 S (1+x+x2 + x2) dx = (Type an integer or a simplified fraction.) -9 Find the average value of the following function over the given interval. Draw a graph of the function and indicate the average value. f(x) = on [1, e] 5 The average value of the function f(x) = (Type an exact answer.) on [1, e) is f =

Answer 1

1. Simplify the expression:

`\\ \sf\:(d)/(dx)\left((dp)/(dx)p^2\right) + (d)/(dp)\left((dp)/(dx)\right)p^2 \\ \\`

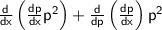
2. Use symmetry to evaluate the integral:

`\\ \sf\:\int_(-9)^(9)(1+x+x^2+x^2) \, dx \\ \\`

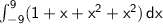
3. Find the average value of the function:

`\\ \sf\:f(x) = 5 \, \text{on} \, [1, e] \\ \\`

Now, let's write the simplified expression, integral, and average value:

1. Simplified expression:

`\\ \sf\:(d)/(dx)\left((dp)/(dx)p^2\right) + (d)/(dp)\left((dp)/(dx)\right)p^2 \\ \\`

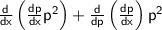
2. Integral using symmetry:

`\\ \sf\:\int_(-9)^(9)(1+x+x^2+x^2) \, dx \\ \\`

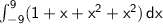
3. Average value of the function:

`\\ \sf\:= (1)/(e-1) \int_(1)^(e) 5 \, dx \\ \\`