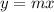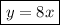Answer:

Explanation:
We can see that this line has a constant of proportionality. That is — x is proportional to y and vice versa. This means that the equation for the line's equation will be in the form:
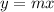
where
 is the ratio of x to y.
is the ratio of x to y.
This ratio is also known as the line's slope. We can solve for the slope using the equation:
slope = rise / run
slope =
 y /
y /
 x
x
slope = 8 / 1
slope = 8

So, the equation of the line is: