The equation is:
⇨ y + 11 = 4(x + 3)
Work/explanation:
Recall that the point slope formula is
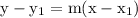 ,
,
where m is the slope and (x₁, y₁) is a point on the line.
Plug in the data:

Simplify.
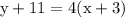
Hence, the point slope equation is y + 11 = 4(x + 3).
Simplified to slope intercept:
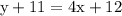
 <- this is the simplified slope intercept equation
<- this is the simplified slope intercept equation