Question

A billboard designer has decided that a sign should have 5-ft margins at the top and bottom and 1-ft margins on the left and right sides. Furthermore, the billboard should have a total area of 8000 ft (including the margins). Printed Region If x denotes the left-right width (in feet) of the billboard, determine the value of x that maximizes the area of the printed region of the billboard. X feet Use this value of x to compute the maximum area of the printed region. Maximum area of printed region = square feet

Answer 1

To find the width x that maximizes the printed area of the billboard, express the height y in terms of x using the total area equation, and differentiate the area of the printed region with respect to x to find the critical points. The maximum area can be computed by substituting the value of x that maximizes the area into the area of the printed region equation.

Step-by-step explanation:

To maximize the area of the printed region within the billboard including the margins, we'll denote the width of the printed area as x and its height as y. Given the 5-ft top and bottom margins, the total height will be y + 10 ft, and considering the 1-ft left and right margins, the total width will be x + 2 ft. The total area of the billboard including margins is 8000 ft2. This can be expressed as:

(​x + 2)(​y + 10) = 8000

Now, we need to express y in terms of x and set up the equation for the area of the printed region, which will simply be x ​⋅ ​y, and find the value of x that maximizes it.

The total area equation can be rearranged to find a relation for y: y = (8000 / (​x + 2)) - 10.

Substituting y back into the area of the printed region, we get:

Area of printed region = x ⋅ ((8000 / (​x + 2)) - 10)

The maximum area of the printed region can be found by differentiating this equation with respect to x and setting the derivative equal to zero to find the critical points. The critical point that makes the second derivative negative will give us the maximum area.

After solving, we'll use the found value of x to compute the maximum area of the printed region.

Answer 2

The value of x maximizing the printed region width is 798 feet. The maximum area of the printed region on the billboard is 7980 square feet.

Given:

- Margins at the top and bottom: 5 feet each

- Margins on the left and right sides: 1 foot each

- Total area of the billboard (including margins): 8000 square feet

The total area of the billboard, including margins, can be expressed as the product of the total height and total width:

Total area = Total height * Total width

The total height considering top and bottom margins is 5 + 5 = 10 feet.

The total width considering left and right margins is x + 2 feet (with 1-foot margins on each side).

So, the equation representing the total area of the billboard is:

8000 = 10 \times (x + 2)

Now, solve for x:

8000 = 10x + 20

10x = 7980

`\[x = (7980)/(10)\]`

x = 798

Therefore, x = 798 feet represents the left-right width of the printed region of the billboard.

To find the maximum area of the printed region, considering this width:

Maximum area = Width × Height

Maximum area
`= \(798 * 10\)`

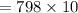
Maximum area
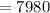`= \(7980\)`square feet

Thus, the maximum area of the printed region on the billboard is 7980 square feet.