Question

URGENT *EASY 10 POINTS* : Show steps to get the expression ln(sqrt(2) +1) - ln(1/sqrt(2)) equal to -ln(1-(1/sqrt2))

Answer 1

Explanation:

To show that the expression
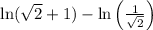`\ln(√(2) + 1) - \ln\left((1)/(√(2))\right)` is equal to
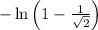`-\ln\left(1 - (1)/(√(2))\right)`, we can simplify both sides of the equation using the properties of logarithms. Here are the steps:

Step 1: Simplify the expression on the left side:

`\ln(√(2) + 1) - \ln\left((1)/(√(2))\right)`

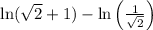
Step 2: Apply the logarithmic property
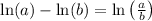`\ln(a) - \ln(b) = \ln\left((a)/(b)\right)` to combine the logarithms:

`\ln\left((√(2) + 1)/((1)/(√(2)))\right)`

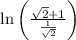
Step 3: Simplify the expression within the logarithm:

`\ln\left(((√(2) + 1))/(\left((1)/(√(2))\right))\right)`

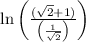
Step 4: Simplify the denominator by multiplying by the reciprocal:

`\ln\left(((√(2) + 1))/(\left((1)/(√(2))\right)) \cdot √(2)\right)`

`\ln\left(((√(2) + 1) \cdot √(2))/(\left((1)/(√(2))\right) \cdot √(2))\right)`

`\ln\left(((√(2) + 1) \cdot √(2))/(1)\right)`

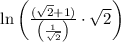
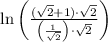
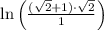
Step 5: Simplify the numerator:

`\ln\left(((√(2) + 1) \cdot √(2))/(1)\right)`

`\ln\left(√(2)(√(2) + 1)\right)`

`\ln\left(2 + √(2)\right)`

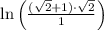
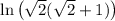
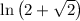
Now, let's simplify the right side of the equation:

Step 1: Simplify the expression on the right side:

`-\ln\left(1 - (1)/(√(2))\right)`

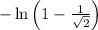
Step 2: Simplify the expression within the logarithm:

`-\ln\left((√(2) - 1)/(√(2))\right)`

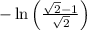
Step 3: Apply the logarithmic property
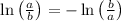`\ln\left((a)/(b)\right) = -\ln\left((b)/(a)\right)` to switch the numerator and denominator:

`-\ln\left((√(2))/(√(2) - 1)\right)`

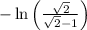
Step 4: Simplify the expression:

`-\ln\left((√(2))/(√(2) - 1)\right)`

`-\ln\left((√(2)(√(2) + 1))/(1)\right)`

`-\ln\left(2 + √(2)\right)`

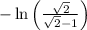
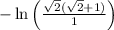
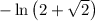
As we can see, the expression
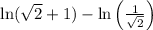`\ln(√(2) + 1) - \ln\left((1)/(√(2))\right)` simplifies to
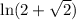`\ln(2 + √(2))`, which is equal to
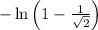`-\ln\left(1 - (1)/(√(2))\right)`.