Question

A ceiling fan with 80-cm-diameter blades is turning at 60 rpm.Suppose the fan coasts to a stop 25s after being turned off.

a.) What is the speed of the trip of a blade 10 s after thefan is turned off?
b.) Through how many revolutions does the fan turn whilestopping?

Answer 1

The linear speed of the blade 10 s after the fan is turned off is 48 m/s. The fan turns through 1500 revolutions while stopping.

Step-by-step explanation:

To solve this problem, we can use the formula for linear speed:

v = ω * r

Where v is the linear speed, ω is the angular speed, and r is the radius of rotation.

a) To find the linear speed of a blade 10 s after the fan is turned off, we need to calculate the angular speed ω at that time and then use the formula above. Since the fan is coasting to a stop, the angular acceleration is negative and we can use the following formula:

ω = ωi + α * t

Where ωi is the initial angular speed, α is the angular acceleration, and t is the time. Given that ωi = 60 rpm and α = 0 (since the fan is coasting), we can substitute these values into the equation and solve for ω:

ω = 60 rpm - 0 * 10 s = 60 rpm

Now, we can calculate the linear speed using the formula:

v = ω * r = 60 rpm * 0.8 m = 48 m/s

So, the linear speed of the blade 10 s after the fan is turned off is 48 m/s.

b) To find the number of revolutions the fan turns while stopping, we can use the formula for angular displacement:

θ = ωi * t + (1/2) * α *
`t^2`

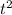
Where θ is the angular displacement, ωi is the initial angular speed, α is the angular acceleration, and t is the time. Since the fan starts at 60 rpm and stops in 25 s, we can substitute these values into the equation:

θ = 60 rpm * 25 s + (1/2) * 0 *
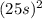`(25 s)^2` = 1500 rpm * s = 1500 rev

So, the fan turns through 1500 revolutions while stopping.

Answer 2

The student's question involves finding the linear speed of a point on a ceiling fan blade 10 seconds after turning off and calculating the total number of revolutions while it stops. Using concepts of rotational kinematics and uniform deceleration, angular velocity is calculated, which is then used to get the linear speed and total revolutions.

Step-by-step explanation:

The student's question involves calculating the linear speed of a point on a ceiling fan blade as it decelerates to a stop and determining the number of revolutions the fan makes whilestopping. We're given that the fan has a diameter of 80 cm and an initial rotational speed of 60 revolutions per minute (rpm). To solve this, we will employ concepts of rotational motion and kinematics. However, since the question does not provide a specific deceleration rate or torque, we assume uniform deceleration over the given time frame of 25 seconds.

a.) To find the rotational speed 10 s after the fan is turned off, we assume a constant deceleration. Let's designate the initial angular velocity as ωi, the final angular velocity as ωf after 25 s which is 0 (since the fan stops), the angular deceleration as α, and the time interval as Δt. First, we calculate α using the formula ωf = ωi + αΔt. Plugging in the values, 0 = (60 rpm)(2π rad/rev)/60 s + α(25 s). We find α and then use it to get the angular velocity 10 s after the fan is turned off. Next, we convert this angular velocity to the linear speed of the tip of a blade, which is at a radius of 40 cm.

b.) The total number of revolutions while stopping is found by integrating the angular speed over the stopping time period from 0 to 25 s. This can be handled using the kinematic equation for angular motion θ = ωit + 0.5αt2, where θ is the total angle covered in radians. We then convert this angle to whole revolutions.