Question

When the dimensions of a cube are doubled, 0 the surface area and the volume are doubled the surface area is doubled and the volume is quadrupled 0 the surface area is quadrupled and the volume is multiplied by 8 the surface area is quadrupled and the volume is multiplied by 6​

Answer 1

Answer: 3

Explanation:

Answer 2

c) If the dimensions of a cube are doubled, the surface area is quadrupled and the volume is multiplied by 8.

Explanation:

The surface area of a cube is the total area of its six faces.

Since all six faces of a cube are congruent squares, the surface area can be calculated by multiplying the length of one side (s) by itself and then multiplying the result by 6.

`\boxed{\textsf{Surface area of a cube}=6s^2}`

The volume of a cube can be calculated by multiplying the length of one side (s) by itself twice, or by raising it to the power of 3.

`\boxed{\textsf{Volume of a cube}=s^3}`

When the dimensions of a cube are doubled, the length of each side becomes twice its original length (2s).

`\begin{aligned}\textsf{Surface area}&=6(2s)^2\\&=6\cdot 2^2 \cdot s^2\\&=6 \cdot 4 \cdot s^2\\&=\boxed{4 \cdot 6s^2}\end{aligned}`

`\begin{aligned}\textsf{Volume}&=(2s)^3\\&=2^3\cdot s^3\\&=\boxed{8\cdot s^3}\end{aligned}`

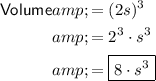
Therefore, if the dimensions of a cube are doubled, the surface area is quadrupled and the volume is multiplied by 8