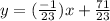Answer:
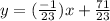
Explanation:
Given equation:
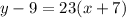
Rewrite it in slope-intercept form:
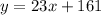
The slope of this line is 23.
The slope of the line perpendicular to it is the negative reciprocal of 23, which is
 .
.
The line passes through the point (2, 3).
Substitute these values into the slope-intercept form (y = mx + b) and solve for the y-intercept (b):

Simplify:
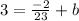
Add
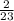 to both sides:
to both sides:
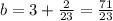
Therefore, the equation of the line that passes through (2, 3) and is perpendicular to
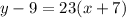 is:
is: