Answer:
Equation:
Explanation:
Step 1:
- Pull out like factors:
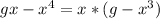
Trying to factor as a Difference of Cubes:
- Factoring:
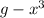
- Theory : A difference of two perfect cubes, a^3 - b^3 can be factored into
- (a-b) • (a^2 +ab +b^2)
- Proof : (a-b)•(a^2+ab+b^2) =
- a^3+a^2b+ab^2-ba^2-b^2a-b^3 =
- a^3+(a^2b-ba^2)+(ab^2-b^2a)-b^3 =
- a^3+0+0-b^3 =
- a^3-b^3
- Check : g^1 is not a cube !!
- Ruling : Binomial cannot be factored as the difference of two perfect cubes
Equation at end of step 1:
Step 2:
- A product of several terms equals zero.
- When a product of two or more terms equals zero, then at least one of the terms must be zero.
- We shall now solve each term = 0 separately
- In other words, we are going to solve as many equations as there are terms in the product
- Any solution of term = 0 solves product = 0 as well.
Solving a Single Variable Equation:
- Solve
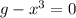
- In this type of equations, having more than one variable (unknown), you have to specify for which variable you want the equation solved.
- We shall not handle this type of equations at this time.
Solution: