Question

Use matrices to determine the coordinates of the vertices of the reflected figure. Then graph the pre-image and the image on the same coordinate grid. Triangle RST with vertices R(-3,7) S(5,3) T(6,-5) reflected over the x axis

Answer 1

To determine the coordinates of the vertices of the reflected figure, we can use a reflection matrix that represents reflection over the x-axis. The reflection matrix is:

`\sf\:\begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \\`

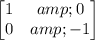
Let's apply this reflection matrix to each vertex of the triangle RST to find the coordinates of the reflected vertices:

For vertex R(-3, 7):

`\sf\:\begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \begin{bmatrix} -3 \\ 7 \\ \end{bmatrix} = \begin{bmatrix} -3 \\ -7 \\ \end{bmatrix} \\`

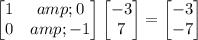
So the reflected coordinates for vertex R are (-3, -7).

For vertex S(5, 3):

`\sf\:\begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix} \begin{bmatrix} 5 \\ 3 \\ \end{bmatrix} = \begin{bmatrix} 5 \\ -3 \\ \end{bmatrix} \\`

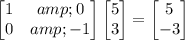
So the reflected coordinates for vertex S are (5, -3).

For vertex T(6, -5):

`\sf\:\begin{bmatrix} 1 & 0 \\ 0 & -1 \\ \end{bmatrix}\begin{bmatrix} 6 \\ -5 \\ \end{bmatrix} = \begin{bmatrix} 6 \\ 5 \\ \end{bmatrix} \\`

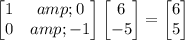
So the reflected coordinates for vertex T are (6, 5).

Now, let's graph the pre-image (triangle RST) and the image (reflected triangle) on the same coordinate grid:

Pre-image (Triangle RST):

• - Vertex R(-3, 7)
• - Vertex S(5, 3)
• - Vertex T(6, -5)

Image (Reflected Triangle):

• - Reflected Vertex R(-3, -7)
• - Reflected Vertex S(5, -3)
• - Reflected Vertex T(6, 5)

You can plot these points on a coordinate grid and connect them to form the triangles.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`